By Oana Ciobotaru, Maxim Peter and Vesselin Velichkov
OpenZeppelin recently identified a critical vulnerability during an audit of Linea‘s PLONK verifier. At its core, the issue is similar in nature to some previously disclosed vulnerabilities (e.g., Frozen Heart, 00). The ‘Last Challenge’ vulnerability arises from the ability of a malicious prover to exploit the degrees of freedom introduced by an incorrect application of the Fiat-Shamir transform when computing the final PLONK challenge. A malicious prover exploiting this vulnerability could steal all the assets in the rollup by submitting a proof for an invalid state transition. While the issue was promptly communicated and fixed, we believe the specifics are worth sharing more broadly so that others may learn to recognize similar patterns and protect themselves accordingly.
Prior to describing the issue in detail below, we give a brief high-level introduction to Zero-Knowledge Succinct Non-interactive ARguments of Knowledge (zkSNARKs) and the Fiat-Shamir transform.
A high-level walkthrough of zkSNARKs
A zkSNARK system involves two parties: a Prover and a Verifier. The Prover aims to convince the Verifier that the result of some computation F is correct, providing a succinct proof that is more efficient to verify than performing the entire computation again. This is especially valuable in the context of a blockchain: instead of having to re-execute all transactions to verify the validity of a state transition, it is cheaper for nodes to verify a zkSNARK proof attesting to the same property. Such a proof can theoretically provide a Layer 2 (L2) with a similar level of security as direct execution on Layer 1 (L1). This comes at the cost of latency but with the benefit of improved scalability.
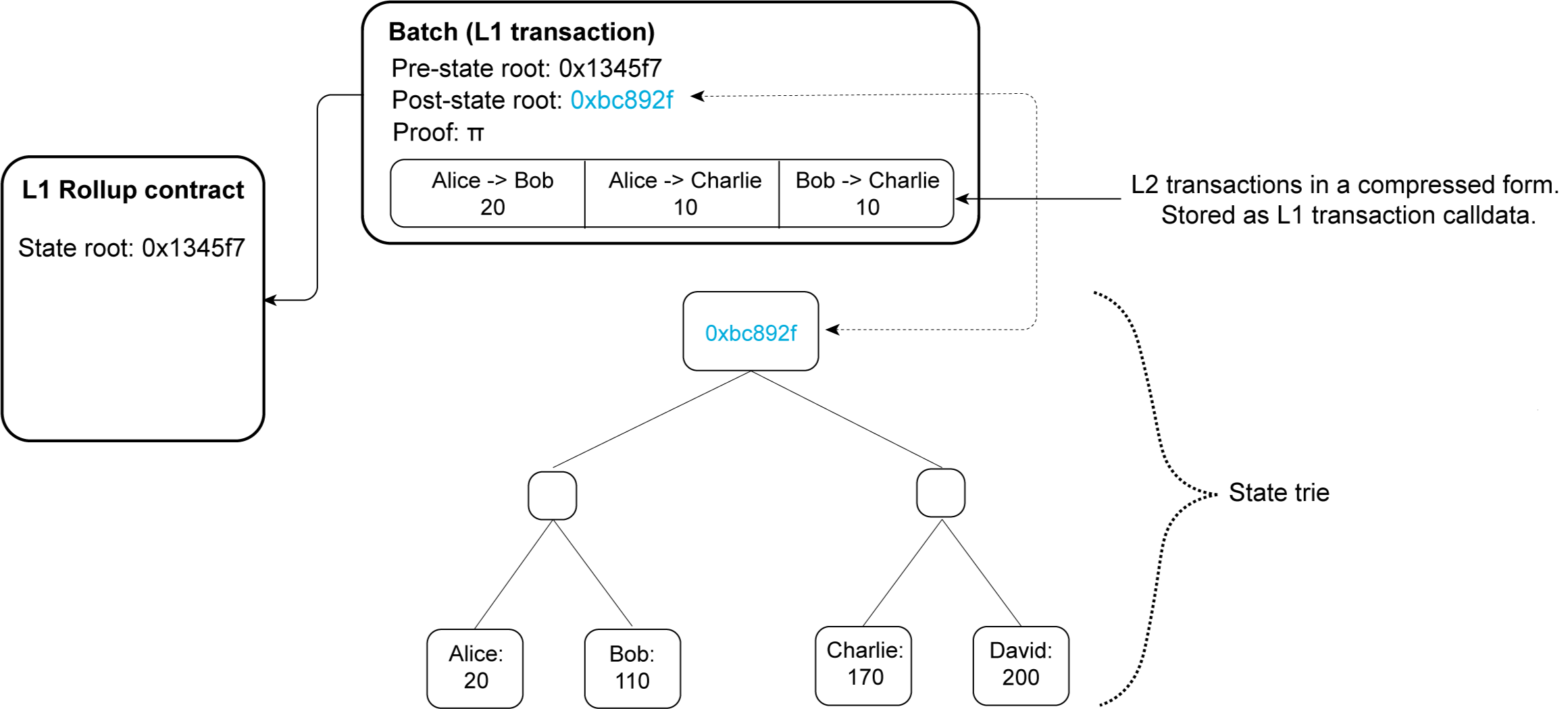
Figure 1: A ZK rollup’s state being updated in its L1 contract (adapted from vitalik.ca)
The computation F mentioned above can be represented as an arithmetic circuit. An arithmetic circuit is a sequence of simple arithmetic operations, such as additions and multiplications, also called gates, connected by wires. The inputs to the circuit are of two types: public values (public input), known by both the Prover and the Verifier, and private values (witness), known only to the Prover and representing the internal values of the computation.
With a zkSNARK, the Prover proves knowledge of the witness without revealing it to the Verifier (i.e., the zero-knowledge property, protecting the honest Prover against a potentially malicious Verifier), and testifies that the computation F was executed correctly (i.e., the soundness property, protecting the honest Verifier against a potentially malicious Prover).

Figure 2: Simple example of an arithmetic circuit with two addition and one multiplication gates
Given such an arithmetic circuit, one would choose an appropriate arithmetisation (e.g., R1CS, AIR, Plonkish) and, implicitly, an NP language for which one would build a zkSNARK scheme. While these details are valuable to any practitioner out there, they are outside the scope of this blog. We recommend the following external resources covering such topics:
- Vitalik’s excellent trio of introductory blog posts (first, second, third)
- Vitalik’s blog post regarding PLONK
- LambdaClass summary on arithmetisation
Going further, a zkSNARK system has two main building blocks: a Polynomial Interactive Oracle Proof (PIOP) and a Polynomial Commitment Scheme. Both of them, in their original form, are interactive, meaning that they proceed as a series of communication rounds between the Prover and the Verifier. Intuitively, a PIOP (with a first version introduced in PLONK and called Polynomial Protocol, and later generalized to PIOP in BFS19) abstracts away, in the form of a set of polynomial identities, the atomic constraints described by the arithmetic circuit. A PIOP is compiled into a zkSNARK system via one of various existing zkSNARK compilers (as described in either PLONK, Marlin, BFS19, etc.) by additionally involving a polynomial commitment scheme.
The interactive nature of the scheme means that the Prover and the Verifier have to wait for each other before moving on to the next step. In practice, interactivity introduces significant latency between the steps and requires a Prover to produce a new proof for each new Verifier.
The Fiat-Shamir Transform
In order to avoid the interactivity bottleneck, there exists the Fiat-Shamir transform. This transform can be applied to any sound and constant round public-coin interactive protocol to yield a functionally equivalent, sound and non-interactive protocol. Note that in a public-coin interactive two-party protocol, all that the interactive Verifier does in terms of communication is to compute random challenges and send them to the interactive Prover.
A simplified example of the Fiat-Shamir transform is given in the figure below.

Figure 3: Fiat-Shamir transform of a simplified interactive protocol
It has been shown that the Fiat-Shamir transform is secure in the random oracle model. In practice, however, the random oracle model is instantiated by a hash function.
Going back to our example introduced in Figure 3, both the Prover and the Verifier use a hash function to compute the challenge c as the hash of the commitment comf and the public input x for that instance. This way, any modification of comf by a malicious Prover would also change c, preventing it from choosing both comf and c to its advantage.
In the following, we will focus on a concrete zkSNARK, namely PLONK. More specifically, we will look at a bug found in the Linea implementation of PLONK’s Fiat-Shamir transform.
PLONK
PLONK is a ZK succinct argument system that, given an arithmetic circuit C, proves that a party (i.e., the Prover) knows a witness w corresponding to a public input x such that (x,w) satisfies the arithmetic circuit C. In most common variants of PLONK, the polynomial commitment is instantiated with a KZG polynomial commitment and the resulting proof is a set of commitments (in fact, the commitments are points on a pairing-friendly elliptic curve) and field elements. The interactive version of PLONK includes several rounds of communication between the Prover and the Verifier.
The protocol can be made non-interactive by using the Fiat-Shamir transform: for each interactive round, the non-interactive PLONK Prover self-generates the corresponding set of challenges by hashing the transcript of the communication up to that round. The transcript up to a certain round is defined as the concatenation of the public parameters that define the circuit, the public inputs that define the instance, and the proof elements computed by the PLONK Prover up to that certain round. The version of PLONK examined in this blog post is the latest one available at the time of writing (from the 17th of August 2022), in which the transcript and the corresponding challenges computed at each round are shown below:

where pp contains the public parameters and the public inputs, while H denotes a hash function.
Notice that u (the last challenge) is not used in any of the PLONK Prover rounds. In fact, u is only used by the PLONK Verifier to batch-validate multiple evaluations at two different evaluation points. Hence, rightfully, the following question arises: given that the PLONK Verifier only needs u to be random and u is not used by the PLONK Prover, does an “efficiency-oriented” Verifier really need to follow the specified protocol and compute u as the hash of the full transcript?
The Last Challenge Attack
In the case of PLONK, not computing the challenges using the full transcript exposes the verifier to potential vulnerabilities. As an example, the Last Challenge Attack is applicable to implementations of the PLONK Verifier in which the last challenge u is not derived using the proof elements [W𝔷]1 and [W𝔷ω]1 (which are part of the full transcript).
Prior to describing the steps of the attack, we briefly recall the relevant part of the PLONK Verifier. The PLONK verifier works in 12 steps, the last of which represents the verification of the following bi-linear pairing equation:

Note that in the equation above, [F]1 and [E]1 are computed by the Verifier using the commitments and evaluations sent by the Prover.
The Last Challenge Attack proceeds as follows:
-1.gif?width=1920&height=1080&name=LastChallenge%20(1)-1.gif)
Implications
In the case of a ZK rollup on Ethereum, the circuit simulates the Ethereum Virtual Machine (EVM). An honest prover can thus prove that blocks of transactions were executed correctly, and a certain state transition is valid. However, a verifier implementation vulnerable to the Last Challenge Attack makes it possible for a malicious prover to forge a proof for an invalid state transition. By doing so, a malicious prover can set itself as the owner of all the assets sitting in the rollup.
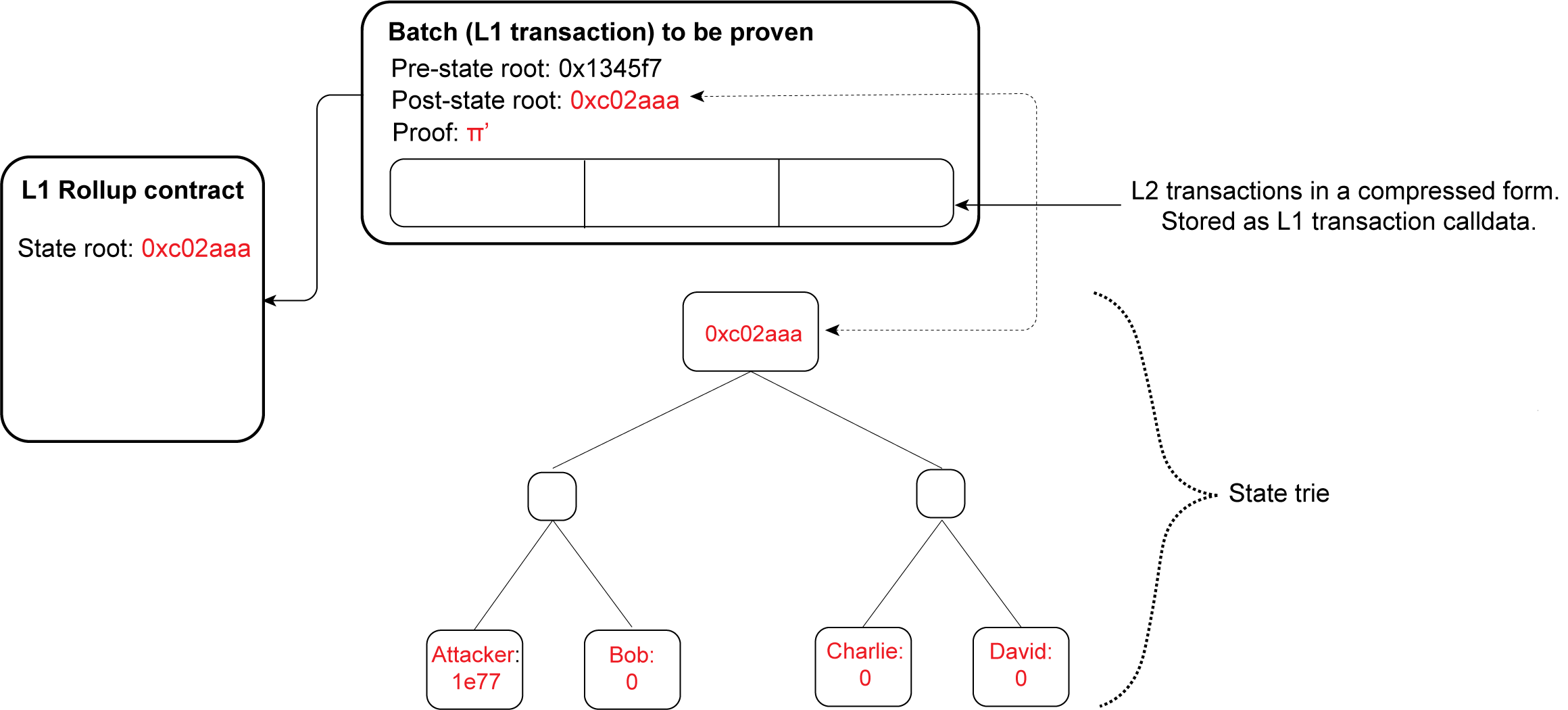
Conclusion
The Fiat-Shamir transform is a common source of security vulnerabilities in zkSNARK systems. Non-interactive verifiers should follow the standard specifications which, in the case of PLONK, derive the Fiat-Shamir challenges from the entire transcript. This derivation ensures that any change to transcript elements by a malicious prover also modifies the challenges. As seen above, deviations from the standard can lead to the construction of proofs of false statements by malicious provers, with potentially disastrous consequences. Mind your Fiat-Shamir's!


